0300.最长递增子序列
题目
给一个整数数组 nums ,找到其中最长严格递增子序列的长度
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列
示例 1:
示例 2:
示例 3:
提示:
1 <= nums.length <= 2500-10^4 <= nums[i] <= 10^4
题解
方法一:动态规划
思路与算法
最容易想到的是暴力搜索
package main
import "fmt"
func lengthOfLIS(nums []int) int {
if len(nums) == 0 {
return 0
}
if len(nums) == 1 {
return 1
}
max_len := 1
for i := 0; i < len(nums); i++ {
max_len = max(max_len, L(nums, i))
}
return max_len
}
func L(nums []int, i int) int {
// Returns the length of longest increasing subsequence ending to index i
max_len := 1
// only one number
if i == 0 {
return 1
}
// 0, 1, 0, 3, 2, 3
// i = 2, nums[i] = 0
// 计算到 0 结束的最长子序列
// 0, 1, 0
for j := 0; j < i; j++ { // nums[i] 必须被选取
if nums[j] < nums[i] {
// 取最大值
max_len = max(max_len, 1+L(nums, j))
}
}
return max_len
}
func main() {
fmt.Printf("%v", lengthOfLIS([]int{0, 1, 0, 3, 2, 3}))
}
定义 \(\textit{dp}[i]\) 为考虑前 \(i\) 个元素,以第 \(i\) 个数字结尾的最长上升子序列的长度,注意 \(\textit{nums}[i]\) 必须被选取
在如上的暴力搜索中对应为
L(0) = 1
L(1) = max{L(0)} + 1 (且 nums[1] > nums[i], i 为取到的 max L 对应的 nums 值)
L(2) = max{L(0), L(1)} + 1 (且 nums[2] > nums[i], i 为取到的 max L 对应的 nums 值)
从小到大计算 \(\textit{dp}\) 数组的值,在计算 \(\textit{dp}[i]\) 之前,已经计算出 \(\textit{dp}[0 \ldots i-1]\) 的值,则状态转移方程为: $$ \textit{dp}[i] = \max(\textit{dp}[j]) + 1, \text{其中} \, 0 \leq j < i \, \text{且} \, \textit{num}[j]<\textit{num}[i] $$
即考虑往 \(\textit{dp}[0 \ldots i-1]\) 中最长的上升子序列后面再加一个 \(\textit{nums}[i]\)。由于 \(\textit{dp}[j]\) 代表 \(\textit{nums}[0 \ldots j]\) 中以 \(\textit{nums}[j]\) 结尾的最长上升子序列,所以如果能从 \(\textit{dp}[j]\) 这个状态转移过来,那么 \(\textit{nums}[i]\) 必然要大于 \(\textit{nums}[j]\),才能将 \(\textit{nums}[i]\) 放在 \(\textit{nums}[j]\) 后面以形成更长的上升子序列
最后,整个数组的最长上升子序列即所有 \(\textit{dp}[i]\) 中的最大值
因此可以实现递归改递推,并且记忆搜索过程中一些计算
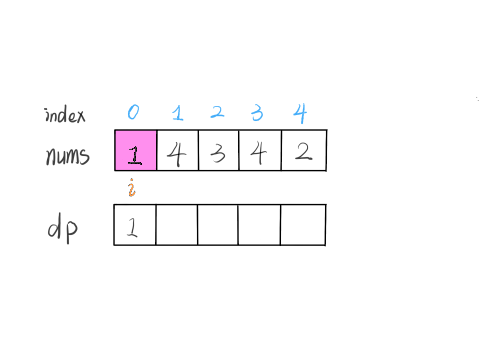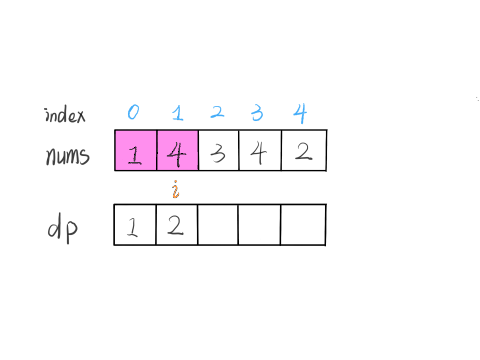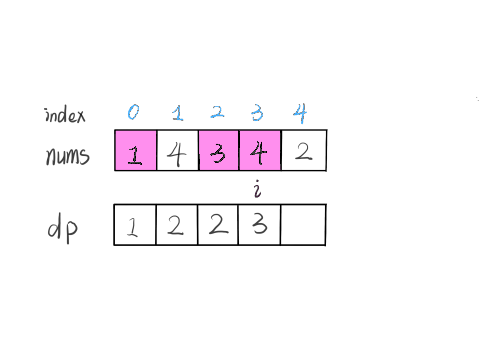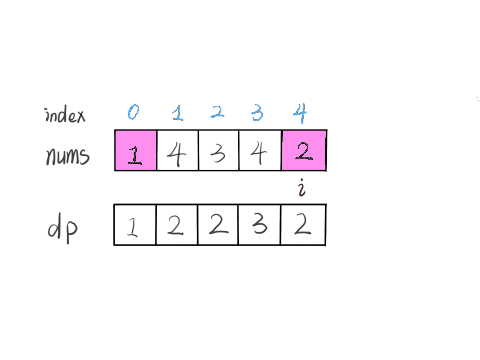
复杂度分析
-
时间复杂度:\(O(n^2)\),其中 \(n\) 为数组 \(\textit{nums}\) 的长度。动态规划的状态数为 \(n\),计算状态 \(dp[i]\) 时,需要 \(O(n)\) 的时间遍历 \(dp[0 \ldots i-1]\) 的所有状态,所以总时间复杂度为 \(O(n^2)\)
-
空间复杂度:\(O(n)\),需要额外使用长度为 \(n\) 的 \(dp\) 数组
代码实现
package main
import "fmt"
func lengthOfLIS(nums []int) int {
if len(nums) == 0 {
return 0
}
dp := make([]int, len(nums))
dp[0] = 1
max_len := 1
for i := 1; i < len(nums); i++ {
dp[i] = 1
// ending to i
for j := 0; j < i; j++ {
if nums[i] > nums[j] {
dp[i] = max(dp[i], dp[j]+1)
}
}
max_len = max(max_len, dp[i])
}
return max_len
}
func main() {
fmt.Printf("%v", lengthOfLIS([]int{0, 1, 0, 3, 2, 3}))
}
方法二:贪心 + 二分查找
思路与算法
考虑一个简单的贪心,如果要使上升子序列尽可能的长,则需要让序列上升得尽可能慢,因此希望每次在上升子序列最后加上的那个数尽可能的小
基于上面的贪心思路,维护一个数组 \(d[i]\) ,表示长度为 \(i\) 的最长上升子序列的末尾元素的最小值,用 \(\textit{len}\) 记录目前最长上升子序列的长度,起始时 \(len\) 为 \(1\),\(d[1] = \textit{nums}[0]\)
同时可以注意到 \(d[i]\) 是关于 \(i\) 单调递增的。因为如果 \(d[j] \geq d[i]\) 且 \(j < i\),考虑从长度为 \(i\) 的最长上升子序列的末尾删除 \(i-j\) 个元素,那么这个序列长度变为 \(j\) ,且第 \(j\) 个元素 \(x\)(末尾元素)必然小于 \(d[i]\),也就小于 \(d[j]\)。那么就找到了一个长度为 \(j\) 的最长上升子序列,并且末尾元素比 \(d[j]\) 小,从而产生了矛盾。因此数组 \(d\) 的单调性得证
依次遍历数组 \(\textit{nums}\) 中的每个元素,并更新数组 \(d\) 和 \(len\) 的值。如果 \(\textit{nums}[i] > d[\textit{len}]\) 则更新 \(len = len + 1\),否则在 \(d[1 \ldots len]\)中找满足 \(d[i - 1] < \textit{nums}[j] < d[i]\) 的下标 \(i\),并更新 \(d[i] = \textit{nums}[j]\)
根据 \(d\) 数组的单调性,可以使用二分查找寻找下标 \(i\),优化时间复杂度
最后整个算法流程为:
-
设当前已求出的最长上升子序列的长度为 \(\textit{len}\)(初始时为 \(1\)),从前往后遍历数组 \(\textit{nums}\),在遍历到 \(\textit{nums}[i]\) 时:
-
如果 \(\textit{nums}[i] > d[\textit{len}]\) ,则直接加入到 \(d\) 数组末尾,并更新 \(\textit{len} = \textit{len} + 1\)
-
否则,在 \(d\) 数组中二分查找,找到第一个比 \(\textit{nums}[i]\) 小的数 \(d[k]\) ,并更新 \(d[k + 1] = \textit{nums}[i]\)
-
以输入序列 \([0, 8, 4, 12, 2]\) 为例:
-
第一步插入 \(0\),\(d = [0]\)
-
第二步插入 \(8\),\(d = [0, 8]\)
-
第三步插入 \(4\),\(d = [0, 4]\)
-
第四步插入 \(12\),\(d = [0, 4, 12]\)
-
第五步插入 \(2\),\(d = [0, 2, 12]\)
最终得到最大递增子序列长度为 \(3\)
复杂度分析
-
时间复杂度:\(O(n\log n)\)。数组 \(\textit{nums}\) 的长度为 \(n\),依次用数组中的元素去更新 \(d\) 数组,而更新 \(d\) 数组时需要进行 \(O(\log n)\) 的二分搜索,所以总时间复杂度为 \(O(n\log n)\)
-
空间复杂度:\(O(n)\),需要额外使用长度为 \(n\) 的 \(d\) 数组
代码实现
额外空间
package main
import (
"fmt"
"sort"
)
func lengthOfLIS(nums []int) int {
g := []int{}
for _, x := range nums {
j := sort.SearchInts(g, x)
if j == len(g) { // >=x 的 g[j] 不存在
g = append(g, x)
} else {
g[j] = x
}
}
return len(g)
}
func main() {
fmt.Printf("%v", lengthOfLIS([]int{0, 1, 0, 3, 2, 3}))
}
原地覆盖
package main
import (
"fmt"
"sort"
)
func lengthOfLIS(nums []int) int {
g := nums[:0] // 原地修改
for _, x := range nums {
j := sort.SearchInts(g, x)
if j == len(g) { // >=x 的 g[j] 不存在
g = append(g, x)
} else {
g[j] = x
}
}
return len(g)
}
func main() {
fmt.Printf("%v", lengthOfLIS([]int{0, 1, 0, 3, 2, 3}))
}
方法三:patience game 的纸牌游戏
思路与算法
其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关,甚至有一种排序方法就叫做 patience sorting(耐心排序)
首先,给你一排扑克牌,像遍历数组那样从左到右一张一张处理这些扑克牌,最终要把这些牌分成若干堆
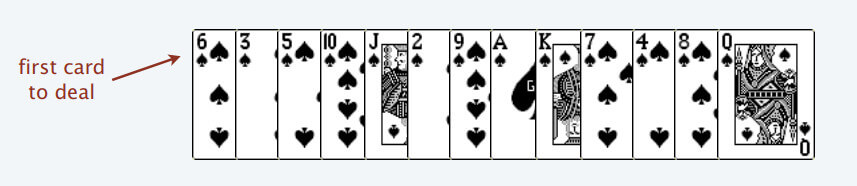
处理这些扑克牌要遵循以下规则:
只能把点数小的牌压到点数比它大的牌上;如果当前牌点数较大没有可以放置的堆,则新建一个堆,把这张牌放进去;如果当前牌有多个堆可供选择,则选择最左边的那一堆放置
比如说上述的扑克牌最终会被分成这样 5 堆(认为纸牌 A 的牌面是最大的,纸牌 2 的牌面是最小的)
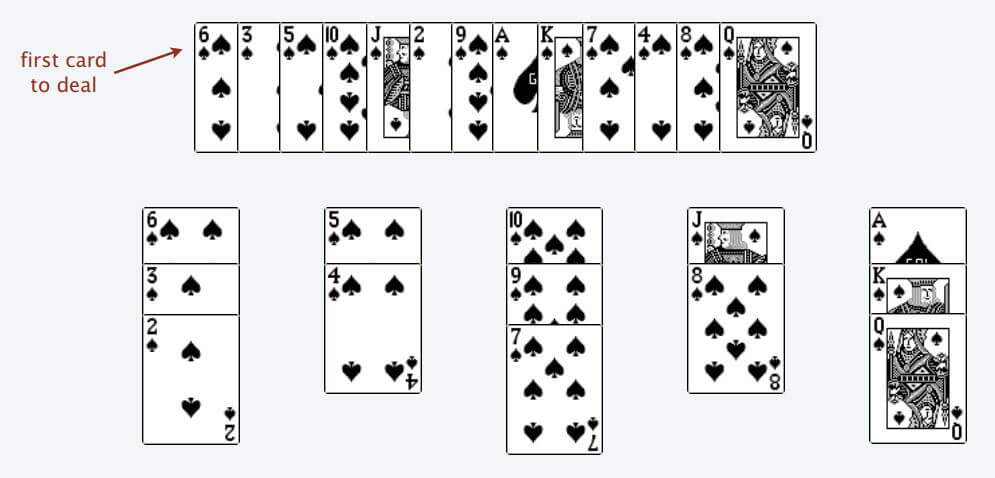
为什么遇到多个可选择堆的时候要放到最左边的堆上呢?因为这样可以保证牌堆顶的牌有序(2, 4, 7, 8, Q)
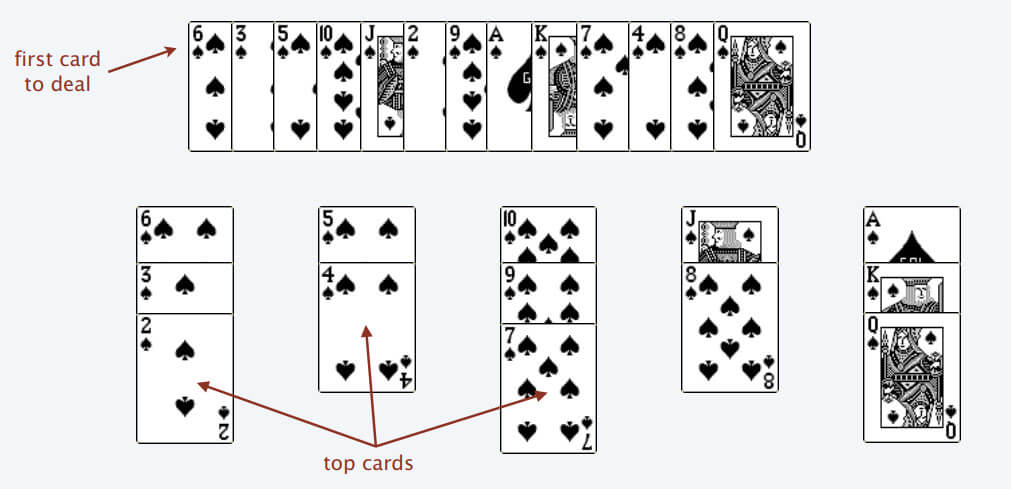
按照上述规则执行,可以算出最长递增子序列,牌的堆数就是最长递增子序列的长度
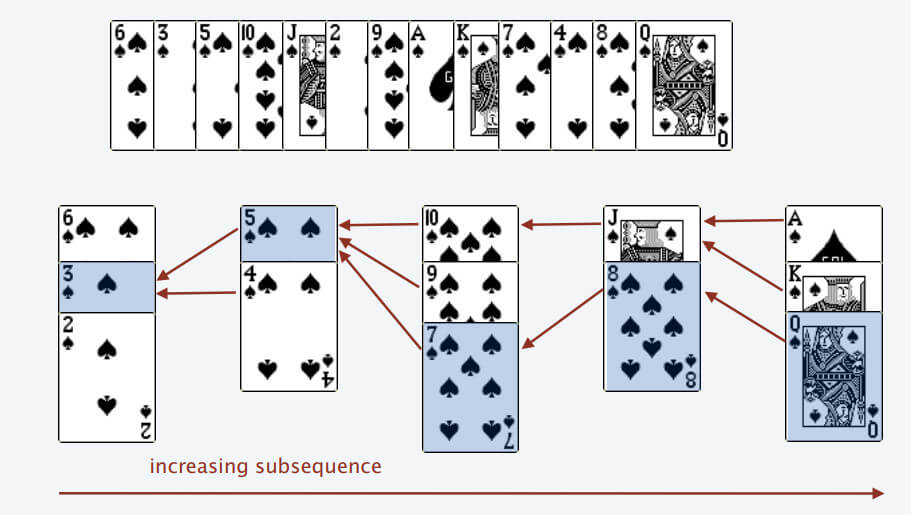
要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗,牌堆顶的牌不是有序吗,这就能用到二分查找了:用二分查找来搜索当前牌应放置的位置
代码实现
package main
import "fmt"
func lengthOfLIS(nums []int) int {
top := make([]int, len(nums))
// 牌堆数初始化为 0
piles := 0
for i := 0; i < len(nums); i++ {
// 要处理的扑克牌
poker := nums[i]
/***** 搜索左侧边界的二分查找 *****/
left, right := 0, piles
for left < right {
mid := (left + right) / 2
if top[mid] > poker {
right = mid
} else if top[mid] < poker {
left = mid + 1
} else {
right = mid
}
}
/*********************************/
// 没找到合适的牌堆,新建一堆
if left == piles {
piles++
}
// 把这张牌放到牌堆顶
top[left] = poker
}
// 牌堆数就是 LIS 长度
return piles
}
func main() {
fmt.Printf("%v", lengthOfLIS([]int{0, 1, 0, 3, 2, 3}))
}