平衡二叉树
平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树, 可以保证查询效率较高
具有以下特点:
- 它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1
- 左右两个子树都是一棵平衡二叉树
平衡二叉树的常用实现方法有 AVL、红黑树、替罪羊树、Treap、伸展树等
在工程中,一般会使用红黑树实现平衡二叉树。但是很多平衡二叉查找树其实并没有严格符合上面的定义(树中任意一个节点的左右子树的高度相差不能大于 1),比如红黑树,它从根节点到各个叶子节点的最长路径,有可能会比最短路径大一倍。如果我们现在设计一个新的平衡二叉查找树,只要树的高度不比 log2n 大很多(以 2 为底 n 的对数,一棵极其平衡的满二叉树或完全二叉树的高度大约是log2n),尽管它不符合我们前面讲的严格的平衡二叉查找树的定义,但我们仍然可以说,这是一个合格的平衡二叉查找树。比如红黑树,它的高度接近 2log2n。
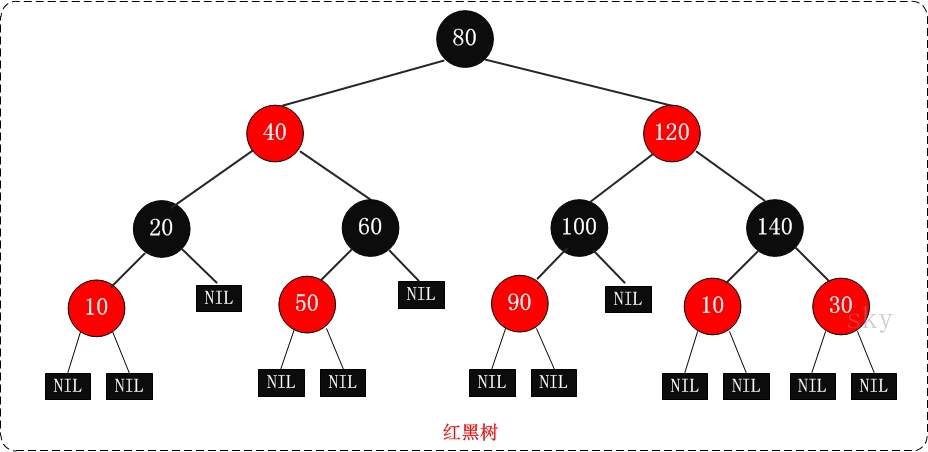
红黑树
红黑树的英文是“Red-Black Tree”,简称R-B Tree。它是一种不严格的平衡二叉查找树。红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
-
根节点是黑色的;
-
每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
为什么使用红黑树而不是AVL树呢?
AVL树严格平衡,虽然查找效率高,但是插入和删除节点效率低,因为要维持平衡而大量调整节点。红黑树只满足近似平衡,要证明红黑树是近似平衡的,我们只需要分析,红黑树的高度是否比较稳定地趋近log2n就好了。红黑树的查找效率只比AVL树低一点,但是插入和删除的效率比AVL高很多。
红黑树的高度只比高度平衡的AVL树的高度(log2n)仅仅大了一倍,而实际上红黑树的总体性能更好。
https://mp.weixin.qq.com/s/qHC3NzJ0sQlfWVbvFft0Vg