二叉搜索树

二叉查找树

二叉查找树（Binary Search Tree）（又：二叉搜索树，二叉排序树）

它或者是一棵空树，或者是具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

二叉搜索树是常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度和树的高度成正比，理想情况下，时间复杂度是 O(logn)。但是，二叉搜索树在频繁动态更新过程中，可能会出现树的高度远大于 logn 的情况，极端情况下二叉树还会退化成链表一样的结构

数列 {1,2,3,4,5,6}，要求创建一颗二叉排序树(BST)：

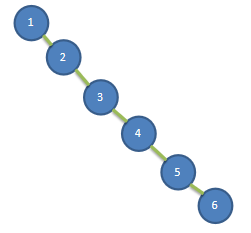
这颗 BST 树存在的问题分析:

• 左子树全部为空，从形式上看，更像一个单链表.
• 插入速度没有影响，但是查询速度明显降低(因为需要依次比较), 不能发挥BST的优势，因为每次还需要比较左子树，其查询速度比单链表还慢

关键字序列

二叉排序树（Binary Search Tree，BST）是一种常见的数据结构，它的每个节点都存储一个关键字，并且满足以下条件：

1. 左子树中所有节点的关键字小于根节点的关键字；
2. 右子树中所有节点的关键字大于根节点的关键字；
3. 左右子树都是二叉排序树

因此，对于给定的关键字序列，可以通过以下步骤构建一棵二叉排序树：

1. 将序列中的第一个关键字作为根节点；
2. 依次将序列中的每个关键字插入到二叉排序树中

具体来说，对于一个关键字 k，从根节点开始，若 k 小于当前节点的关键字，则将其插入到当前节点的左子树中；否则，将其插入到当前节点的右子树中。插入完成后，继续处理下一个关键字，直到序列中的所有关键字都插入到二叉排序树中。

需要注意的是，如果关键字序列本身已经有序，那么构建出的二叉排序树将是一棵单支树，效率会比较低。因此，在实际应用中，为了使二叉排序树的高度尽可能小，可以采用一些随机化的方法，比如随机打乱关键字序列的顺序，或者选择一个随机的关键字作为根节点。这样可以使得二叉排序树的平均高度接近 \(\log_{2}{n}\)，其中 n 是关键字的数量。