图的存储结构

邻接矩阵

图的邻接矩阵（Adjacency Matrix)存储方式是用两个数组来表示图

一个一维的数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息 $$ \operatorname{arc}[i][j]=\left{\begin{array}{l} 1, \text { 若 }\left(v_{i}, v_{j}\right) \in E \text { 或 }\left\langle v_{i}, v_{j}\right\rangle \in E \ 0, \text { 反之 } \end{array}\right. $$ 无向图示例：

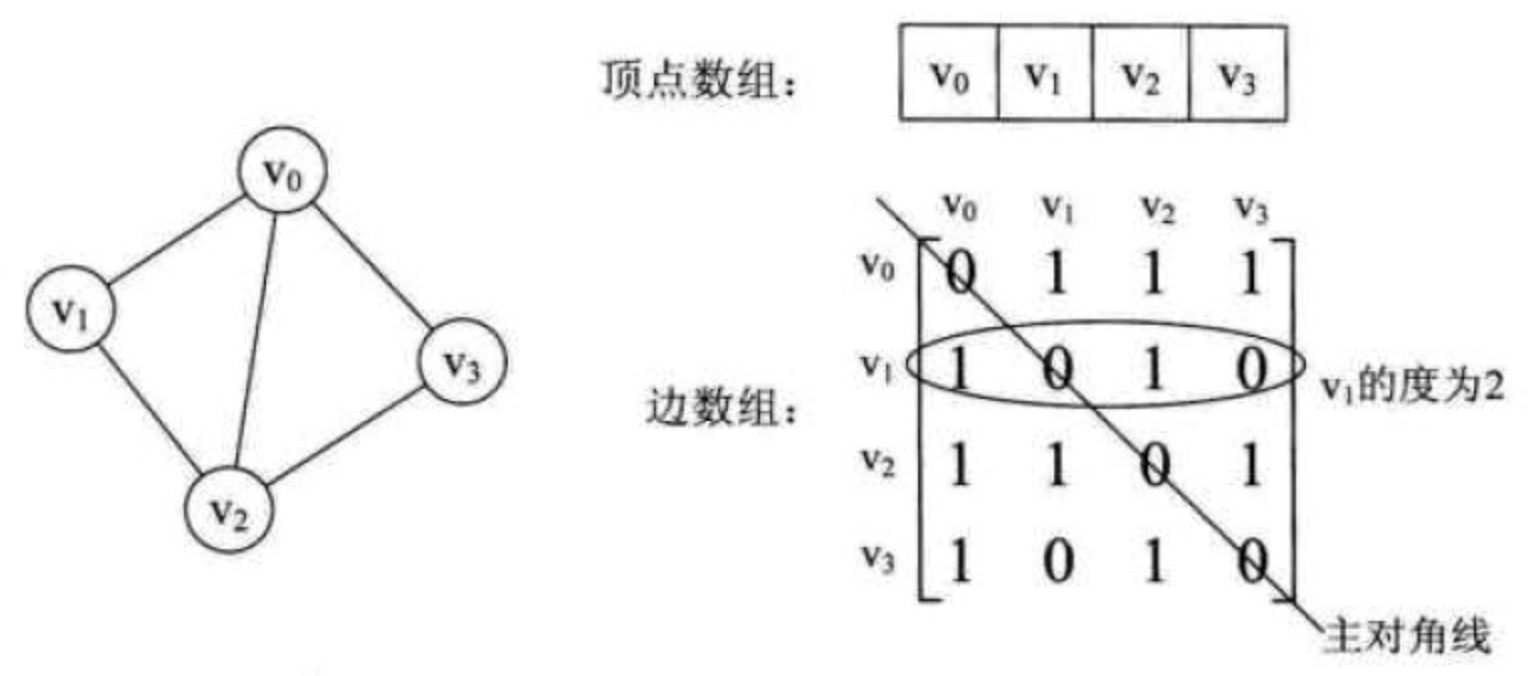
有向图示例：

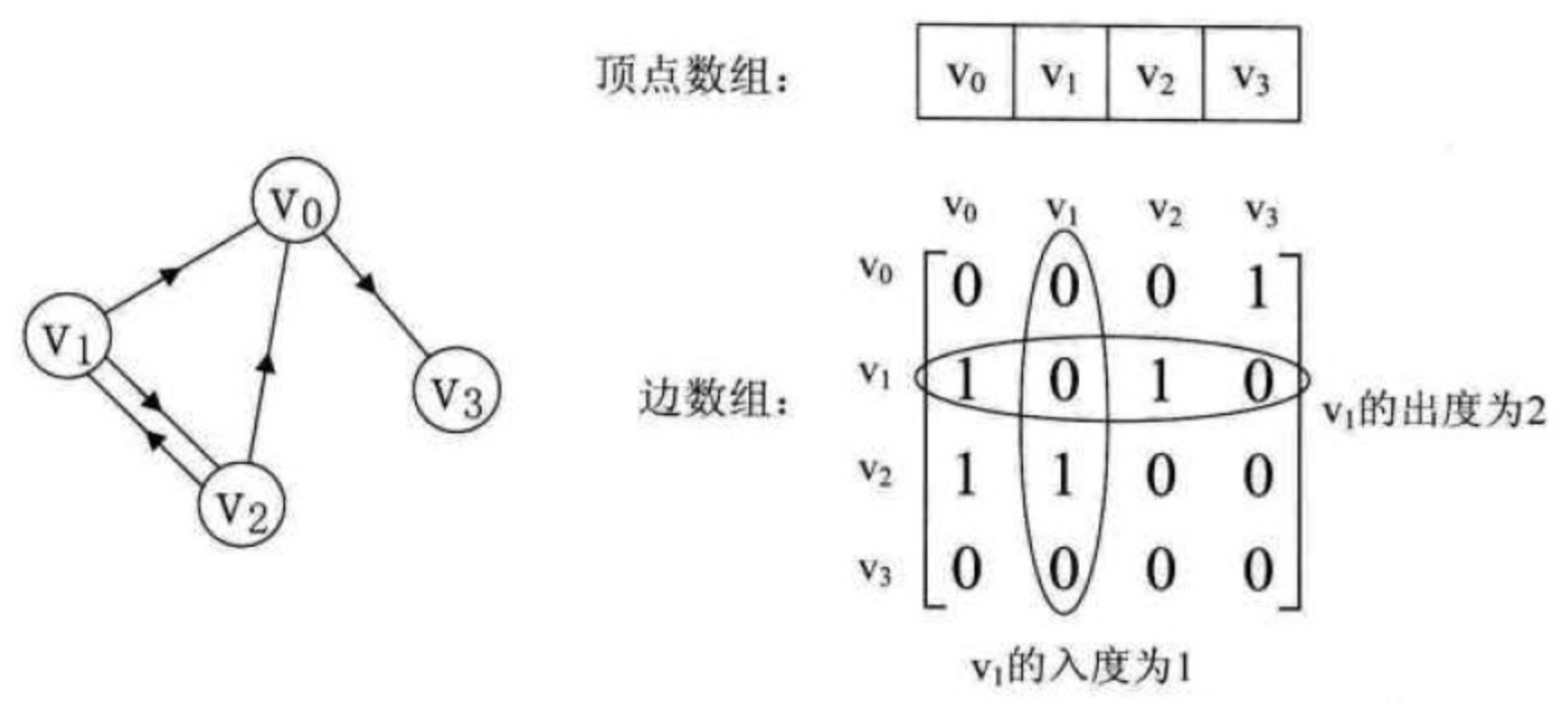
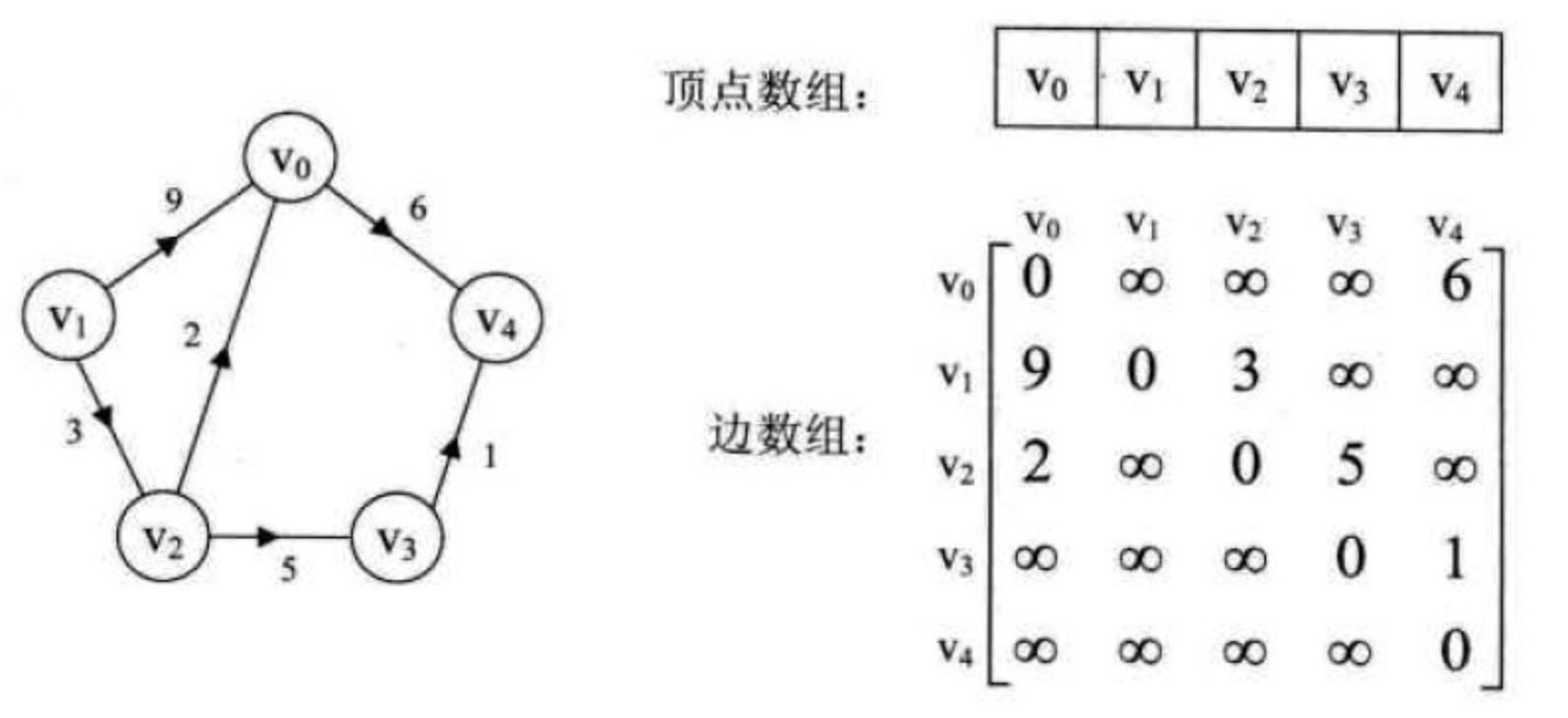
对于带权的图，需要保存权值 $$ \operatorname{arc}[i][j]=\left{\begin{array}{l} W{ij}, \text { 若 }\left(v_{i}, v_{j}\right) \in E \text { 或 }\left\langle v_{i}, v_{j}\right\rangle \in E \ 0, \text { 若 i = j } \ \infty, \text { 反之 } \end{array}\right. $$

每条边上都带有权的有向图：